Support Vector Machine

Pengertian Support Vector Machine (SVM)

    Support Vector Machine–selanjutnya disebut SVM–adalah metode pada machine learning yang dapat digunakan untuk menganalisis data dan mengurutkannya ke dalam salah satu dari dua kategori. SVM ditemukan oleh Vladimir N. Vapnik dan Alexey Ya. Chervonenkis pada tahun 1963. Sejak itu, SVM telah digunakan dalam klasifikasi teks, hiperteks dan gambar. SVM dapat bekerja dengan karakter tulisan tangan dan algoritma ini telah digunakan di laboratorium biologi untuk melakukan tugas seperti menyortir protein. Algoritma ini juga dikenal sebagai Support Vector Network (SVN).

    SVM bekerja untuk mencari hyperplane atau fungsi pemisah (decision boundary) terbaik untuk memisahkan dua buah kelas atau lebih pada ruang input. Hiperplane dapat berupa line atau garis pada dua dimensi dan dapat berupa flat plane pada multiple plane. 

Jenis-Jenis Algoritma SVM

SVM dapat dibagi menjadi 2 jenis yakni:

1.    SVM Linear

    SVM linear digunakan untuk data yang dapat dipisahkan secara linear, yang berarti jika sebuah dataset dapat diklasifikasi menjadi dua kelas dengan menggunakan sebuah garis lurus tunggal, maka data tersebut disebut sebagai data yang dapat dipisahkan secara linear, dan classifier yang digunakan disebut sebagai Linear SVM classifier.

2.    SVM Non-linear

    SVM non-linear digunakan untuk data yang dapat dipisahkan secara non-linear, yang berarti jika sebuah dataset tidak dapat diklasifikasi menggunkan garis lurus, maka data tersebut disebut data non-linear dan classifier yang digunakan disebut sebagai Non-linear SVM classifier.

Kelebihan Support Vector Machine

• Cocok untuk ruang dimensi tinggi
• Efektif untuk kasus dimana jumlah dimensi lebih besar dari jumlah sampel
• Hemat memori, karena menggunakan training point dari fungsi keputusan (support vector)
• Bekerja relatif baik ketika ada margin pemisahan yang jelas antar kelas.

Kelemahan Support Vector Machine

• Algoritma SVM tidak cocok untuk dataset dalam jumlah yang besar karena membutuhkan waktu training yang lama.
• SVM tidak bekerja dengan baik ketika dataset memiliki lebih banyak noise misalnya kelas target terjadi tumpang tindih.
• Jika jumlah fitur untuk setiap titik data melebihi jumlah sampel data training, SVM akan memiliki performa yang kurang baik
• Karena support vector classifier bekerja dengan meletakkan titik data di atas dan di bawah hyperplane, tidak ada kejelasan probabilistik untuk klasifikasi tersebut. Hal ini dapat menyebabkan beban komputasi yang tinggi.

Hyperplane, Support Vector, dan Max Margin pada Algoritma SVM

Hyperplane

    Dalam memisahkan kelas dalam ruang n-dimensi, ada kemungkinkan terdapat beberapa garis atau batas keputusan. Namun perlu menemukan batas keputusan terbaik yang membantu mengklasifikasikan titik data. Batas terbaik ini dikenal sebagai hyperplane dari SVM.

    Hyperplane adalah batas keputusan yang membedakan dua kelas dalam SVM. Titik data yang jatuh di kedua sisi hyperplane dapat dikaitkan dengan kelas yang berbeda.

    Dimensi hyperplane bergantung pada fitur yang ada pada dataset, yang artinya jika terdapat dua fitur, maka hyperplane akan berbentuk garis lurus. Dan jika terdapat tiga fitur, maka hyperplane akan menjadi bidang dua dimensi.

Berikut adalah contoh ilustrasi hyperplane

Support Vector

    Support vector ialah titik data atau vektor yang paling dekat dengan hyperplane dan yang mempengaruhi posisi hyperplane. Karena vektor-vektor ini mendukung hyperplane, maka disebut support vector.

Max Margin

    Margin adalah jarak antara support vector dari masing-masing kelas di sekitar hyperplane. Pada gambar dibawah, margin diilustrasikan dengan jarak antara 2 garis putus. Margin terbesar (max margin) dapat ditemukan dengan memaksimalkan nilai jarak antara hyperplane dan titik terdekatnya. 

    Dapat dilihat pada gambar bagian kanan memiliki margin lebih besar daripada gambar bagian kiri. Secara intuitif, margin yang lebih besar akan menghasilkan performa klasifikasi yang lebih baik. 

Cara Kerja Algoritma SVM

    Algoritma SVM bekerja dengan cara memetakan data ke ruang fitur berdimensi tinggi sehingga titik data dapat dikategorikan, bahkan ketika data tersebut tidak dapat dipisahkan secara linier.

    Apabila pemisah antar kategori berhasil ditemukan, data dapat ditransformasikan sedemikian rupa sehingga pemisah tersebut dapat digambarkan sebagai hyperplane. Kemudian, karakteristik data baru dapat digunakan untuk memprediksi pada kelompok mana record baru seharusnya berada.

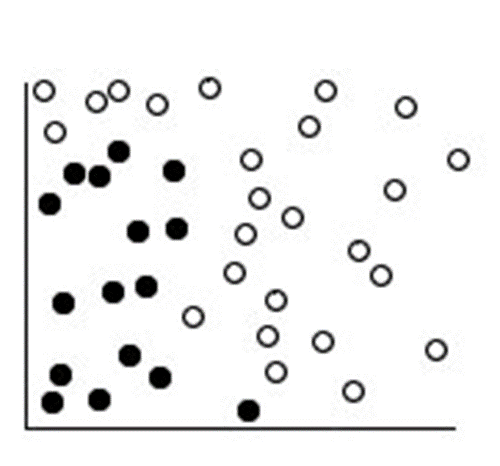
    Sebagai ilustrasi, perhatikan gambar di bawah dimana terdapat titik-titik data yang terpisah dalam 2 kategori, yakni bulatan hitam dan bulatan putih.

    Kedua kategori tersebut kemudian dipisahkan dengan kurva, seperti yang terlihat pada gambar 2

    Setelah dilakukan transformasi, batas antara dua kategori dapat ditentukan oleh hyperplane, seperti yang ditunjukkan gambar 3